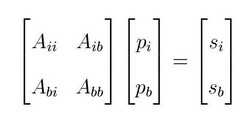Utilisation de l'IBM Blue Gene/P de l'IDRIS : Le projet SEISCOPE

Modélisation numérique de la propagation des ondes sismiques en domaine fréquentiel fondée sur un solveur hybride (direct/itératif) massivement parallèle (projet SEISCOPE)

Responsable : Stéphane Operto¹

Participants et collaborations : H. Ben Hadj Ali¹, L. Giraud², A. Haidar³, F. Sourbier¹, J. Virieux⁴

• ¹: UMR Géosciences Azur / CNRS / UNSA / IRD / OCA.
• ² ENSEEIHT-IRIT, Toulouse.
• ³ CERFACS, Toulouse.
• ⁴ LGIT - Université Joseph Fourier, Grenoble.

L?imagerie sismique du sous-sol par inversion du champ d?onde complet nécessite des méthodes performantes de modélisation des ondes acoustiques/élastiques dans des milieux géologiques 3D. Un algorithme massivement parallèle de modélisation des ondes a été implémenté dans le domaine des fréquences et porté sur la machine Babel de l?IDRIS. Dans le domaine fréquentiel, la modélisation des ondes se ramène à la résolution d?un grand système d?équations linéaires creux dont la solution est le champ d?onde monochromatique et le terme de droite est la source. La résolution du système est fondée sur une décomposition en domaine utilisant un solveur hybride direct/itératif et une approche par complément de Schur. Un processeur est alloué à chaque sous-domaine. Le solveur itératif GMRES est utilisé pour résoudre le système réduit du complément de Schur fournissant les valeurs du champ aux points d?interface entre les sous-domaines. Le solveur direct est utilisé en séquentiel sur chaque processeur pour calculer le terme de droite du système de Schur et les valeurs du champ aux points intérieurs. La scalabilité temps de cette approche, sa précision en fonction du critère d?arrêt des itérations et son coût mémoire ont été quantifiés. L?implémentation d?un second niveau de parallélisme dans le code de simulation est programmé.

La prospection sismique est une des principales méthodes géophysiques pour l?imagerie du sous-sol. Les méthodes d?inversion du champ d?onde complet sont des optimisations numériques consistant à minimiser l?écart entre les données sismiques enregistrées par un dispositif de sources et de capteurs et les données calculées dans un modèle initial du sous-sol (Pratt et al., 1998). L?inversion peut s?implémenter dans le domaine temporel ou fréquentiel. La formulation fréquentielle fournit un cadre adapté pour une imagerie multi-échelle procédant des basses fréquences vers les hautes fréquences. Par ailleurs, seules quelques fréquences sont nécessaires pour focaliser l?image du sous-sol sous réserve de dispositifs de sources et de capteurs suffisamment étendus. Nous avons évalé une méthode de modélisation 3D des ondes acoustiques dans le domaine fréquentiel adaptée à des applications d?imagerie par inversion des formes d?onde. Dans le domaine fréquentiel, la modélisation des ondes se ramène à la résolution d?un grand système d?équations linéaires creux dont la solution est le champ d?onde monochromatique et le terme de droite est la source sismique. Pour des applications d?imagerie, ce système doit être résolu pour un grand nombre de sources c?est-à-dire de seconds membres. L?approche développée est fondée sur une méthode de décomposition en domaine intégrant un solveur hybride direct/itératif et une approche par complément de Schur. Les avantages et inconvénients de l?approche hybride représentent un compromis entre ceux des deux approches extrêmes fondées sur un solveur direct ou itératif en termes de coût mémoire, « scalabilité », simulations multi seconds membres et conditionnement du système.

L?équation d?onde pour des milieux acoustiques 3D s?exprime sous forme matricielle dans le domaine des fréquences, B(x,y,z,?) p = s, eq. 1, où elle représente une généralisation de l?équation d?Helmholtz. B est la matrice d?impédance dont les coefficients dépendent de la fréquence et des propriétés du milieu. p est le champ scalaire de pression, s est la source. L?équation d?onde est discrétisée par une méthode aux différences finies (Operto et al., 2007). L?approche utilisée pour résoudre le système (1) est une méthode de décomposition en domaines fondée sur un solveur hybride direct/itératif et une approche par complément de Schur (Saad, 2002). Le modèle du sous-sol est décomposé en sous-domaines avec un recouvrement de 1 (Fig. 1a). Si l?on considère un seul niveau de parallélisme, un processeur est alloué à chaque sous-domaine. Dans l?approche par complément de Schur, les inconnues sont subdivisées en deux catégories: les inconnues pi intérieures à chaque sous-domaine et les inconnues pb situées aux interfaces entre deux sous-domaines voisins. Les inconnues sont ordonnées suivant cette classification ce qui conduit au système 2 suivant :

La matrice B_ii est une matrice bloc diagonale où chaque bloc correspond à un sous-domaine : toute résolution de système impliquant B_ii se ramène à la résolution d?un système local sur chaque processeur. L?élimination de p_i dans la seconde équation du système 2 conduit au système du complément de Schur. Nous utilisons dans un premier temps le solveur itératif GMRES pour résoudre ce système réduit préconditionné qui fournit la solution pour p_b. Nous en déduisons p_i à partir de la première équation du système 2. Le solveur direct MUMPS est utilisé en séquentiel sur chaque processeur pour factoriser les blocs de la matrice B_ii. Le solveur itératif GMRES effectue à chaque itération des produits matrice-vecteur impliquant le complément de Schur. Ces produits sont naturellement parallèles car ils s?expriment comme la somme de produits locaux sur chaque processeur. Le préconditionneur du système de Schur est la somme des inverses des compléments de Schur locaux assemblés sur chaque processeur. Cet assemblage ne nécessite que quelques communications point-à-point. La « scalabilité » de l?approche est contrôlée par le nombre de sous-domaines. En effet, plus le nombre de sous-domaines augmente, plus la précision du préconditionneur se dégrade et le nombre d?itérations de GMRES augmente. Par contre, chaque processeur effectue à chaque itération un nombre d?opérations moins important lorsque le nombre de sous-domaines augmente en raison de la diminution de la taille des sous-domaines. Nous avons évalué le nombre optimal de sous-domaines fournissant le meilleur compromis entre ces deux comportements antagonistes. La complexité mémoire de l?approche est O(N⁴/k) où N est la dimension d?une grille cubique 3D et k le nombre de sous-domaines dans une direction. Le coût mémoire décroit avec le nombre de sous-domaines (i.e., avec le nombre de processeur), un avantage indéniable comparativement à des approches fondées sur l?utilisation exclusive d?un solveur direct. Les perspectives de développement sont l?implémentation d?un deuxième niveau de parallélisme dans le code appliqué à chaque sous-domaine auquel est alloué un groupe de processeurs (Haidar, 2008) et d?optimiser les phases de calcul du préconditionneur (communication de L. Giraud).

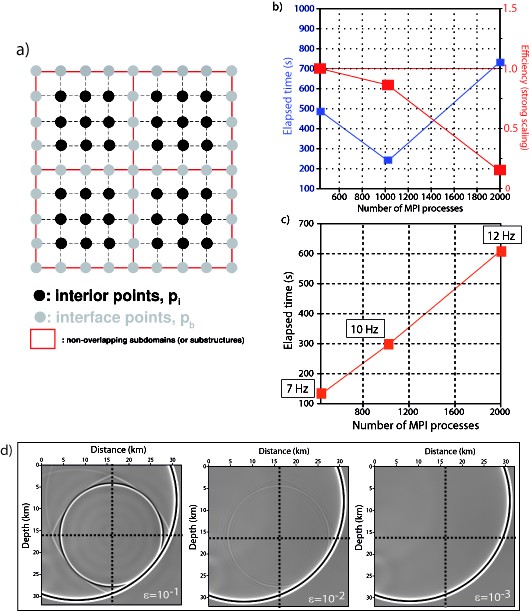
Nous avons évalué la « scalabilité » de la méthode à l?aide du modèle synthétique SEG/EAGE overthrust (Operto et al., 2007). Les simulations ont été effectuées sur un nombre croissant de processeurs pour évaluer l?évolution du nombre d?itérations de GMRES et du temps calcul avec le nombre de sous-domaines. La taille de la grille est 87 x 338 x 338 correspondant à 10 millions d?inconnues dans le système 1. Les simulations ont été effectuées sur 442, 1024 et 2000 processeurs. Les courbes d?accélération et d?efficacité sont représentées sur la Figure 1b pour le mode « strong scaling ». L?efficacité est proche de 1 jusqu?à un nombre critique de processeurs au delà duquel le temps calcul augmente en raison de la dégradation du préconditioneur. Nous avons également effectué des simulations pour des fréquences de plus en plus élevées en adaptant le pas de la grille à la fréquence. Pour chaque fréquence, le nombre de processeurs minimisant le temps calcul est utilisé (442, 1000, 2000). Le temps calcul est reporté sur la Figure 1c pour 3 fréquences 7, 10 et 12 Hz correspondant à 3 grilles numériques de taille croissante. Nous constatons une augmentation linéaire du temps calcul avec la taille du problème (test en mode « weak scaling »).

L?utilisation de GMRES nécessite la définition d?un critère d?arrêt des itérations en fonction de la précision requise par l?application considérée. La Figure 1d montre une simulation dans un milieu homogène 2D subdivisé en 4 sous-domaines pour 3 valeurs du critère d?arrêt. Nous observons des diffractions et des réfractions parasites aux frontières des sous-domaines lorsque ce critère d?arrêt est trop élevé (?=10^-1). ?=10^-3 fournit une solution vierge d?artefact. ?=10^-2 fournit un compromis acceptable entre précision et temps calcul pour des applications d?imagerie.

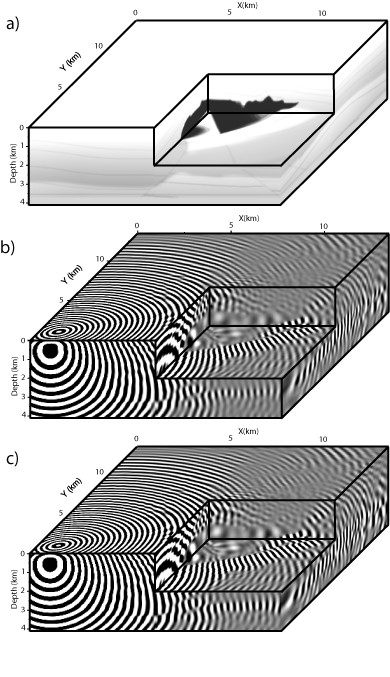
Pour vérifier la convergence de la méthode pour des milieux caractérisés par de forts contrastes de propriétés physiques, nous avons effectué une simulation dans le modèle SEG/EAGE Salt contenant un corps de sel dans un encaissant sédimentaire. La dimension de la grille est 120 x 372 x 372 corrrespondant à 16.6 millions d?inconnues. Le nombre de processeurs est égal à 576 répartis en 12 x 12 x 4 sous-domaines. La taille de chaque sous-domaine est 31 x 31 x 31 et permet d?effectuer une factorisation LU séquentielle sur chaque processeur en utilisant 2 Go de mémoire par processeur en mode SMP. Le nombre d?itérations était de 113 et 283 pour ?=10^-2 et ?=10^-3. Le temps calcul était de 682 s pour ?=10^-3. Le champ de pression monochromatique à 7 Hz calculé par l?approche hybride est comparé à celui calculé avec un code différences finies temps-espace fondé sur un schéma d?intégration explicite en temps et dont la solution monochromatique a été extraite par transformée de Fourier discrète.

Figure 1 : a) Décomposition en domaine avec un recouvrement de 1 pour une grille aux différences finies. Quatre sous-domaines délimités par les lignes rouges sont illustrés. b) Temps de simulation (bleu) et efficacité (rouge) pour une simulation effectuée sur 442, 1024 et 2000 processeurs. Les deux premières simulations ont été effectuées en mode SMP et la dernière en mode DUAL. Le nombre d?itérations était 732, 1325 et 2223. La taille des sous domaines était respectivement de 29 x 28 x 28, 21 x 21 x 21 et 17 x 17 x 17. Le nombre total d?inconnues était égal à 10 millions. c) Temps écoulé en fonction de la taille du problème. Le nombre de processeurs fourni en abscisse est adapté à la taille du problème pour minimiser le temps calcul (voir Fig. b). d) Illustration de la sensibilité de la solution par rapport au critère d?arrêt des itérations. Des fronts d?onde parasites sont excités aux frontières des sous-domaines indiquées par les pointillés si les itérations sont stoppées trop tôt.

Figure 2 :  a) Modèle de vitesse salt de la SEG/EAGE.  b) Champ de pression monochromatique pour une fréquence de 7 Hz calculé avec le solveur hybride.  c) Champ de pression monochromatique pour une fréquence de 7 Hz calculé avec un code de différences finies. La solution monochromatique est extraite par transformée de Fourier discrète.

F. Sourbier, A. Haidar, L. Giraud, S. Operto and J. Virieux, Frequency-domain Full-waveform modeling using a hybrid direct/iterative solver based on parallel domain decomposition method: a tool for full-waveform inversion. Expanded abstracts. SEG Las Vegas Annual meeting, Society of Exploration Geophysics. 2008, pages 2147-2151.     F. Sourbier, A. Haidar, L. Giraud, S. Operto and J. Virieux, Frequency-domain acoustic wave modeling using a hybrid direct/iterative solver based on parallel domain decomposition method. Expanded abstracts. 70th EAGE Conference, Roma. 2008, H036.     F. Sourbier, A. Haidar, L. Giraud, S. Operto and J. Virieux, Combining direct and iterative solvers for improving efficiency of solving wave equations when considering multi-source problems. Expanded abstracts. 70th EAGE Conference, Workshop 8, Computing Trends in O&G, Roma. 2008.

• A. Haidar, On the parallel scalability of hybrid linear solvers for large 3D problems, Thèse de l?INPT, 2008, Toulouse.    
• Ben Hadj Ali, H., S. Operto, et al. (2008). Velocity model building by 3D frequency-domain full-waveform inversion of wide-aperture seismic data. Geophysics 73: VE101-VE117.    
• Operto, S., J. Virieux, et al. (2007). 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver: a feasibility study. Geophysics 72(5): P SM195-SM211.    
• Saad, Y., Ed. (2003). Iterative methods for sparse linear systems. Philadelphia, SIAM.